Chapter 3
PLAYING WITH NUMBERS
Exercise 3.1
Sum No :1
Write all the factors of the following numbers:
(a) 24 (b) 15 (c) 21 (d) 27 (e) 12 (f) 20 (g) 18 (h) 23 (i) 36
Solution.
(a) 24
24 = 1 x 24 , 24 = 2 x 12 , 24 = 3 x 8 , 24 = 4 x 6
Therefore, all the
factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24.
(b) 15
15 = 1 x 15 , 15 = 3 x 5
Therefore, all the
factors of 15 are: 1, 3, 5 and 15.
(c) 21
21 = 1 x 21
21 = 3 x 7
Therefore, all the
factors of 21 are: 1, 3, 7 and 21.
(d) 27
27 = 1 x 27
27 = 3 x 9
Therefore, all the
factors of 27 are: 1, 3, 9 and 27.
(e) 12
12 = 1 x 12
12 = 2 x 6
12 = 3 x 4
Therefore, all the
factors of 12 are: 1, 2, 3, 4, 6 and 12.
(f) Factors of 20
are:
20 = 1 x 20
20 = 2 x 10
20 = 4 x 5
Therefore, all the
factors of 20 are: 1, 2, 4, 5, 10 and 20.
(g) Factors of 18
are:
18 = 1 x 18
18 = 2 x 9
18 = 3 x 6
Therefore, all the
factors of 18 are: 1, 2, 3, 6, 9 and 18.
(h) F+
actors of 23
are:
23 = 1 x 23
Therefore, all the
factors of prime number 23 are: 1 and 23.
(i) 36
36 = 1 x 36
36 = 2 x 18
36 = 3 x 12
36 = 4 x 9
36 = 6 x 6
Therefore, all the
factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18 and 36.
Sum No: 2
2. Write first five multiples
of:
(a) 5
(b) 8
(c) 9
Solution:
(a) 5
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
Therefore, five
multiples of 5 are: 5, 10, 15, 20 and 25.
(b) First five
multiples of 8 are:
8 x 1 = 8;
8 x 2 = 16;
8 x 3 = 24;
8×4 = 32;
8 x 5 = 40
Therefore, five
multiples of 8 are: 8, 16, 24, 32 and 40.
(c) First five
multiples of 9 are:
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
Therefore, five
multiples of 9 are: 9, 18, 27, 36 and 45.
Sum No:3
Match the items in column 1
with the items in column 2.
Column
1
Column 2
(i)
35
(a) Multiple of 8
(ii)
15
(b) Multiple of 7
(iii) 16 (c) Factor of 30
(iv)
20
(v)
25
Solution:
(i) 35 (b) Multiple of 7 (∵ 7 x 5 = 35)
(ii) 15 (c) Factor of 30 (∵ 15 x 2 = 30)
(iii) 16 (a) Multiple of 8 (∵ 8 x 2 = 16)
(iv) 20 (e) Factor of 20 (∵ 20 x 1 = 20)
(v) 25 (d) Factor of 50 (∵ 25 x 2 = 50)
Sum No: 4
Find all the multiples of 9
upto 100.
Solution:
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
9 x 11 = 99
Therefore, all the
multiples of 9 upto 100 are:-
9, 18, 27, 36, 45,
54, 63, 72, 81, 90 and 99
Exercise 3.2
Sum No.1
What is the sum of any two:
(a) Odd numbers?
(b) Even numbers?
Solution:
(a) The sum of any
two odd numbers is always even.
For Example: 3 + 5
= 8
25 + 17 = 42
(b) The sum of any
two even numbers is always even.
For Example:
8 + 6 = 14
20 + 16 = 36
Sum No.2
State whether the following
statements are True or False.
(a) The sum of three
odd numbers is even.
(b) The sum of two
odd numbers and one even number is even.
(c) The product of
three odd numbers is odd.
(d) If an even
number is divided by 2, the quotient is always odd.
(e) All prime
numbers are odd.
(f) Prime numbers
do not have any factors.
(g) Sum of two
prime numbers is always even.
(h) 2 is only the
even prime number.
(i) All even
numbers are composite numbers.
(j) The product of
any two even numbers is always even.
Solution:
(а) False; sum of
the three odd numbers is always odd.
For example: 5 + 9
+ 17 = 31
(b) True; sum of
two odd numbers and one even number is always even
For example: 5 + 3 + 14 = 22
(c) True; product
of three odd numbers is always odd.
For example: 9 x 5 x 15 = 675
(d) False; If an
even number is divided by 2, then the quotient can either be an odd or an even
number.
For example: 8 ÷ 2 = 4 (even)
And 6÷ 2 = 3 (odd)
(e) False; 2 is a
prime number but it is even.
(f) False; 1 and
the number itself are the factors of each prime number.
For example: 3 = 3
x 1
Thus, 1 and 3 are
the factors of 3.
(g) False; sum of
two prime numbers can either be an odd or an even.
For example: 5 + 2
= 7 (odd)
And 3 + 5 = 8 (even)
(h) True; 2 is
only the even prime number.
(i) False; 2 is
the smallest even number which not composite. It is prime number.
(j) True; product
of any two even numbers is always even.
Sum No.3
The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers up to 100.
Solution:
Pairs of prime
numbers having same digits are:
17 and 71
37 and 73
79 and 97
Sum No.4
Write down separately the
prime and composite numbers less than 20.
Solution:
Prime numbers less
than 20 are:
2, 3, 5, 7, 11,
13, 17 and 19
Composite numbers
less than 20 are:
4, 6, 8, 9, 10,
12, 14, 15, 16 and 18
Sum No.5
What is the greatest prime
number between 1 and 10?
Solution:
Prime numbers
between 1 and 10 are: 2, 3, 5, 7
Thus the greatest
prime number between 1 and 10 is 7.
Sum No.6
Express the following as the sum of two odd primes.
(a) 44 (b) 36 (c) 24 (d) 18
Solution:
(a) 44 = 31 +13
(b) 36 = 31 + 5
(c) 24 = 19 + 5
(d) 18 = 13 + 5
Sum No:7
Give three pairs of prime
numbers whose difference is 2.
[Remark: Two prime
numbers whose difference is 2 are called twin primes]
Solution:
Three pairs of
prime numbers whose difference is 2 are:
3 and 5
5 and 7
11 and 13
Sum No:8
Which of the following
numbers are prime?
(a) 23 (b) 51 (c) 37 (d) 26
Solution:
(a) 23
23 = 1 x 23
Therefore, it is a
prime number.
(b) 51
51 = 1 x 51
51 = 17 x 3
Therefore, it is
not a prime number.
(c) 37
37 = 1 x 37
Therefore, it is a
prime number.
(d) 26
26 = 1 x 26
26 = 13 x 2
Therefore, it is
not a prime number.
Sum No: 9
Write seven consecutive
composite numbers less than 100 so that there is no prime number between them.
Solution.
There are seven
composite numbers between 89 and 97 such that there is no prime number between
them. These seven composite numbers are:
90, 91, 92, 93,
94, 95 and 96
Sum No:10
Express each of the
following numbers as the sum of three odd primes.
(a) 21 (b) 31 (c) 53 (d) 61
Solution:
(a) 21 = 3 + 5 +
13
(b) 31 = 5 + 7 +
19
(c) 53 = 13 + 17 +
23
(d) 61 = 11 + 19 +
31
Sum No:11
Write five pairs of prime
numbers less than 20 whose sum is divisible by 5.
(Hint: 3 + 7 = 10)
Solution:
Required pairs of
prime numbers below 20 whose sum is divisible by 5 are:
<2 and 3> 2 + 3 = 5, divisible by 5
<2 and 13> 2 + 13 =
15,
<3 and 17> 3 + 17 =
20,
<7 and 13> 7 + 13 =
20,
<9 and 11> 9 + 11 =
20,
Sum No:12
Fill in the blanks.
(a) A number which
has only two factors is called a ______ .
(b) A number which
has more than two factors is called a ______.
(c) 1 is neither
______ nor ______.
(d) The smallest
prime number is ______.
(e) The smallest
composite number is ______.
(f) The smallest
even number is ______.
Solution:
(a) prime number
(b) composite
number
(c) a prime
number, a composite number
(d) 2
(e) 4
(f) 2
Exercise 3.3
1. Using divisibility tests,
determine which of the following numbers are divisible by 2; by 3, by 4, by 5,
by 6, by 8, by 9, by 10, by 11 (Say, Yes or No)
|
Number |
Divisible by |
||||||||
|
2 |
3 |
4 |
5 |
6 |
8 |
9 |
10 |
11 |
|
|
128 990 1586 275 6686 639210 429714 2856 3060 406839 |
Yes ….. ….. ….. ….. ….. ….. ….. ….. ….. |
No ….. ….. ….. ….. ….. ….. ….. ….. ….. |
Yes ….. ….. ….. ….. ….. ….. ….. ….. ….. |
No ….. ….. ….. ….. ….. ….. ….. ….. ….. |
No ….. ….. ….. ….. ….. ….. ….. ….. ….. |
Yes ….. ….. ….. ….. ….. ….. ….. ….. ….. |
No ….. ….. ….. ….. ….. ….. ….. ….. ….. |
No ….. ….. ….. ….. ….. ….. ….. ….. ….. |
No ….. ….. ….. ….. ….. ….. ….. ….. ….. |
Solution.
|
Number |
Divisible by |
||||||||
|
2 |
3 |
4 |
5 |
6 |
8 |
9 |
10 |
11 |
|
|
128 990 1586 275 6686 639210 429714 2856 3060 406839 |
Yes Yes Yes No Yes Yes Yes Yes Yes No |
No Yes No No No Yes Yes Yes Yes Yes |
Yes No No No No No No Yes Yes No |
No Yes No Yes No Yes No No Yes No |
No Yes No No No Yes Yes Yes Yes No |
Yes No No No No No No Yes No No |
No Yes No No No No Yes No Yes No |
No Yes No No No Yes No No Yes No |
No Yes No Yes No Yes No No No No |
Sum No.2
Using divisibility tests,
determine which of following numbers are divisible by 4; by 8.
(a) 572 (b) 726352 (c) 5500 (d) 6000 (e) 12159
(f) 14560 (g) 21084 (j) 2150 (h) 31795072 (i) 1700
Solution.
Divisible by 4:- If the number formed by its last two digits (i.e ones and tens ) are divisible by 4. And if the number formed by the last three digits is divisible by 8.
(a) 572
To check divisibility by 4
Here, last two digits form 72
which is divisible by 4 so the number 572 is also divisible by 4.
To check divisibility by 8
Here, last three digits form
572 which is not divisible by 8 so the number 572 is not divisible by 8.
(b) 726352
To check divisibility by 4
Here, last two digits form 52
which is divisible by 4. So the number 726352 is also divisible by 4.
To check divisibility by 8
Here, last three digits form
352 which is divisible 8 so the number 726352 is also divisible by 8.
(c) 5500
To check divisibility by 4
Here, last two digits form 00
which is divisible. Hence, 5500 is divisible by 4.
To check divisibility by 8
Here, last three digits form
500 which is not divisible by 8 so the number 5500 is not divisible by 8.
(d) 6000
To check divisibility by 4
Here, last two digits form 00 which is divisible by 4. Hence, 6000 is divisible by 4.
To check divisibility by 8
Here, , last three digits form 000 which is divisible by 8. Hence, 6000 is divisible by 8.
(e) 12159
To check divisibility by 4
Here, last two digits form 59
which is not divisible by 4 so the number 12159 is not divisible by 4.
To check divisibility by 8
Here, last three digits form
159 which is not divisible by 8 so the number 12159 is not divisible by 8.
(f) 14560
To check divisibility by 4
Here, last two digits form 60
which is divisible by 4 so the number 60 is also divisible by 4.
To check divisibility by 8
Here, last three digits form
560 which is divisible by 8 so the number 14560 is divisible by 8.
(g) 21084
To check divisibility by 4
Here, last two digits form 84
which is divisible by 4 so the number 21084 is also divisible by 4.
To check divisibility by 8
Here, last three digits form
084 which is not divisible by 8 so 21084 is not divisible by 8.
(h) 31795072
To check divisibility by 4
Here, last two digits form 72
which is divisible by 4 so the number is also divisible by 4.
To check divisibility by 8
Here, last three digits form
072 which us divisible by 8 so the number 31795072 is also divisible by 8.
(i) 1700
To check divisibility by 4
Here, last two digits form 0
which is divisible by 4 so the number 1700 is also divisible by 4.
To check divisibility by 8
Here, last three digits form
700 which is not divisible by 8 so the number 1700 is also not divisible
by 8.
(j) 2150
To check divisibility by 4
Here, last two digits form 50
which is not divisible by 4 so the number 2150 is also not divisible by 4.
To check divisibility by 8
Here, last three digits form
150 which is not divisible by 8 so the number 2150 is not divisible by 8.
Sum No. 3:-
Using divisibility tests,
determine which of the following numbers are divisible by 6:
(a) 297144 (b) 1258 (c) 4335 (d) 61233 (e) 901352
(f) 438750 (g) 1790184 (h) 12583 (i) 639210 (j) 17852
Solution:
Divisible by 6:- If a number is divisible by both 2 and 3 then it is divisible by 6 also .
Divisible by 2:-If any of the digits 0, 2, 4, 6 or 8 in its ones place.
Divisible by 3:- If the sum of digits is multiply by 3.
(a) 297144
Here the digit at ones place
is 4 which is even so 297144 is divisible by 2.
The sum of all the digits of
297144 = 2 + 9 + 7 + 1 + 4 + 4 = 27 which is divisible by 3.
Hence, the given number 297144
is divisible by 6.
(b) 1258
Here the digit at ones place
is 8 which is even so 1258 is divisible by 2.
The sum of all digits of 1258
= l + 2 + 5 + 8 = 16 which is not divisible by 3.
Since the given number 1258 is
not divisible by both 2 and 3 therefore, it is not divisible by 6.
(c) 4335
Here the digit at ones place
is 5 which is not even so 4335 it is not divisible by 2.
Hence, 4335 it is also not divisible
by 6.
(d) 61233
Here, the digit at ones place
is 3 which is not even so the number 61233 is not divisible by 2.
Hence, the number 61233 is not
divisible by 6.
(e) 901352
Here, the digit at ones place
is 2 which is even so the number 901352 is divisible by 2.
The sum of all the digits of
901352 = 9 + 0 + 1 + 3 + 5 + 2 = 20 which is not divisible by 3.5
Since, the number 901352 is
not divisible by both 2 and 3 so it is not divisible by 6.
(f) 438750
Here, the digit at ones place
of the given number is 0 so the number 438750 is divisible by 2.
The sum of all the digits of
438750 = 4 + 3 + 8 + 7 + 5 + 0 = 27 which is divisible by 3.
Hence, the given number is
divisible by 6.
(g) 1790184
Here, the digit at ones place
is 4 which is even so the number 1790184 is divisible by 2.
The sum of all the digits of
1790184 = 1 + 7 + 9 + 0 + 1 + 8 + 4 = 30 which is divisible by 3.
Hence, the given number is
divisible by 6.
(h) 12583
Here, the digit at ones place
is 3 which is odd so the number 12583 is not divisible by 2.
Hence, the number 12583 is not
divisible by 6.
(i) 639210
Here, the digit at ones place
is 0 so the number 639210 is divisible by 2.
The sum of all the digits of
639210 = 6 + 3 + 9 + 2 + 1 + 0 = 21 which is divisible by 3.
Hence, the given number is divisible
by 6.
(j) 17852
The digit at ones place of the
given number is 2 which is divisible by 2.
The sum of all the digits of
17852 = 1 + 7 + 8 + 5 + 2 = 23 which is not divisible by 3.
Since, the number 17852 is not
divisible by both 2 and 3 so it is not divisible by 6.
Sum No.4:-
Using divisibility tests,
determine which of the following numbers are divisible by 11:
(a) 5445 (b) 10824 (c) 7138965 (d) 70169308 (e) 10000001 ()901153
Solution.
Find the difference between the sum of the digits at odd places
(from the right) and the sum of the digits at even places (from the right) of
the number. If the difference is either 0 or divisible by 11, then the number is divisible by 11.
(a) 5445
Sum of the digits at odd
places = 5 + 4 = 9
Sum of the digits at even
places = 4 + 5 = 9
Difference = 9 – 9 = 0
Hence, the given number 5445
is divisible by 11.
(b) 10824
Sum of the digits at odd
places = 4 + 8 + 1 = 13
Sum of the digits at even
places = 2 + 0 = 2
Difference = 13 – 2 = 11 which
is divisible by 11.
Hence, the given number 10824
is divisible by 11.
(c) 7138965
Sum of the digits at odd
places = 5 + 9 + 3 + 7 = 24
Sum of the digits at even
places = 6 + 8 + 1 = 15
Difference = 24 – 15 = 9 which
is not divisible by 11.
Hence, the given number
7138965 is not divisible by 11.
(d) 70169308
Sum of all the digits at odd
places = 8 + 3 + 6 + 0 = 17
Sum of all the digits at even
places = 0 + 9 + 1 + 7 = 17
Difference = 17-17 = 0
Hence, the given number
70169308 is divisible by 11.
(e) 10000001
Sum of all the digits at odd
places = 1 + 0 + 0 + 0 = 1
Sum of all the digits at even
places = 0 + 0 + 0 + 1 = 1
Difference = 1 – 1 = 0
Hence, the given number
10000001 is divisible by 11.
(f) 901153
Sum of all the digits at odd places = 9+1+5 = 15
Sum of all the digits at even places = 0+1+3 =4
Difference = 15-4= 11
Hence the given number 901153 is not divisible by 11.
Sum No.5:-
Write the smallest digit and the greatest digit in the blank space of each of the following numbers so that the number formed is divisible by 3.
(a) ____ 6724
(b) 4765 ____ 2
Solution:
We know that number is
divisible by 3 if the sum of all its digits is also divisible by 3.
(a) ___ 6724
Sum of the given digits = 4 +
2 + 7 + 6 = 19
After 19 the next number which
is multiple of 3 is 21.
So, the smallest digit to be
placed is blank space = 21 – 19 = 2
Now, the greatest digit to be
placed in blank space = 8
Such that the sum = 19 + 8 =
27 is divisible by 3.
Thus, the smallest digit = 3
And the greatest digit = 8
(b) 4765 ____ 2.
Sum of the given digits = 2 +
5 + 6 + 7 + 4 = 24 which is divisible 3.
So, the smallest digits to be
placed in blank space = 0
Such that, sum = 24 + 0 = 24
is divisible by 3.
Now, the greatest digit to be
placed in blank space = 9.
Such that the sum = 24 + 9 =
33 which is divisible by 3.
Thus, the smallest digit = 0
And the greatest digit = 9.
Sum No.6:-
Write a digit in the blank space of each of the following numbers so that the numbers formed is divisible by 11.
(a) 92 ___ 389
(b) 8 ___ 9484
Solution.
We know that a number is
divisible by 11 if the difference between the sum of the digits at odd places
(from the right) and the sum of the digits at even places (from the right) of
the number is either 0 or divisible by 11.
(a) 92 ___ 389
Let p be the digit to be
placed in blank space.
Then sum of the digits at odd
places = 9 + 3 + 2 = 14
Sum of the digits at even
places = 8 + p + 9 = 17 + a
Difference = 17 + p – 14 = a +
3
As the difference should be
either 0 or divisible by 11
If p + 3 = 0
Then p = –3 but negative value
cannot be placed in blank space.
So, p + 3 = 11
∴ p = 11 – 3 = 8
So, the required digit = 8
(b) 8 ___ 9484
Let p be the digit to be
placed in blank space.
Sum of the digits at odd
places = 4 + 4 + p = 8 + p
Sum of the digits at even
places = 8 + 9 + 8 = 25
∴ Difference = 25 – (8 + p)
= 25 – 8 – p
= 17 – p
As the difference should be
either 0 or divisible by 11
So, either 17 – p = 0
Then p = 17 which is not
possible.
So we take 17 – p = 11
∴ p = 17 – 11 = 6
So, the missing digit = 6
Exercise 3.4
Sum No .1:-
Find the common factors of:
(a) 20 and 28 (b) 15 and 25 (c) 35 and 50 (d) 56 and 120
Solution.
(a) 20 and 28
Factors of 20 = 1, 2, 4, 5, 10, 20
Factors of 28 = 1, 2, 4, 7, 28
Hence, the common factors of
20 and 28 = 1, 2, 4
(b) 15 and 25
Factors of 15 = 1, 3, 5,
15
Factors of 25 = 1, 5, 25
Hence, the common factors of
15 and 25 = 1, 5
(c) 35 and 50
Factors of 35 = 1, 5, 7, 35
Factors of 50 = 1, 2, 5, 10,
25, 50
Hence, the common factors of
35 and 50 = 1, 5
(d) 56 and 120
Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56
Factors of 120 = 1, 2, 3, 4,
5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Hence, the common factors of
56 and 120 = 1, 2, 4, 8
Sum No.2.
Find the common factors of:
(a) 4, 8 and 12 (b) 5, 15 and 25
Solution.
(a) 4, 8 and 12
Factors of 4 = 1, 2, 4
Factors of 8 = 1, 2, 4, 8
Factors of 12 = 1, 2, 3, 4, 6, 12
Hence, the common factors of
4, 8 and 12 = 1, 2, 4
(b) 5, 15 and 25
Factors of 5 = 1, 5
Factors of 15 = 1, 3, 5, 15
Factors of 25 = 1, 5, 25
Hence, the common factors of
5, 15 and 25 = 1, 5
Sum No.3:-
Find first three common
multiples of:
(a) 6 and 8
(b) 12 and 18
Solution:
(a) 6 and 8
Multiples of 6 = 6, 12, 18,
24, 30, 36, 42, 48, 54, 60, 66, 72
Multiples of 8 = 8, 16, 24,
32, 40, 48, 56, 64, 72
So the first three common
multiples of 6 and 8 = 24, 48, 72
(b) 12 and 18
Multiples of 12 = 12, 24, 36,
48, 50, 72, 84, 96, 108
Multiples of 18 = 18, 36, 54,
72, 90, 108
So the first three common
multiples of 12 and 18 = 36, 72, 108
Sum No. 4:-
Write all the numbers less than 100 which are common multiples of 3 and 4.
Solution.
Multiples of 3 less than 100
are = 3, 6, 9, 12, 15, 18, 21, 24, 27,……, 96, 99
Multiples of 4 less than 100
are = 4, 8, 13, 16, 20, 24, 28, 32, ………, 96
Hence, the common multiples of
3 and 4 less than 100 are: 12, 24, 36, 48, 60, 72, 84 and 96.
Sum No.5:-
Which of the following
numbers are co-prime?
(a) 18 and 35
(b) 15 and 37
(c) 30 and 415
(d) 17 and 68
(e) 216 and 215
(f) 81 and 16
Solution:-
We know that any two numbers
are said to be co-prime if they have only 1 as their common factor.
(a) 18 and 35
Factors of 18 are 1, 2, 3, 6,
9, 18
Factors of 35 are 1, 5, 7, 35
Since, the common factor of 18
and 35 is only 1
Hence, they are co-prime.
(b) 15 and 37
Factors of 15 are 1, 3, 5, 15
Factors of 37 are 1, 37
Since, the common factor of 15
and 37 is only 1.
Hence, they are co-prime.
(c) 30 and 415
Factors of 30 are 1, 2, 3, 5,
6, 15, 30
Factors of 415 are 1, 5, 83
Since, the common factor of 30
and 415 are 1 and 5
Hence, they are not co-prime.
(d) 17 and 68
Factors of 17 are 1, 17
Factors of 68 are 1, 2, 4, 17,
34, 68
Since, the common factor of 17
and 68 are 1 and 17
Hence, they are not co-prime.
(e) 216 and 215
Factors of 216 are 1, 2, 3, 4,
6, 8, 9, 12, 18, 24, 36, 54, 72, 108, 216
Factors of 215 are 1, 5, 43
Since the common factor of 216
and 215 is only 1
Hence, they are co-prime.
(f) 81 and 16
Factors of 81 are 1, 3, 9, 27,
81
Factors of 16 are 1, 2, 4, 8,
16
Since the common factor of 81
and 16 is only 1
Hence, they are co-prime.
Sum No.6:-
A number is divisible by
both 5 and 12. By which other will that number be always divisible?
Solution:-
Factors of 5 = 1, 5
Factors of 12 = 1, 2, 3, 4, 6,
12
Thus 5 and 12 are co-prime
numbers so the number will be divisible by the product 5 × 12 = 60.
So, the given number will
always be divisible by 60.
Sum No.7:-
A number is divisible by 12. By what other will that number be divisible?
Solution:-
If number is divisible by
another number, then it is also divisible by each of the factors of that
number.
Here, factors of 12 are 1, 2,
3, 4, 6, 12
Hence the number which is
divisible by 12 will also be divisible by 1, 2, 3, 4, 6 and 12.
Exercise 3.5
Sum No.1
Which of the following
statements are true?
(a) If a number is divisible
by 3, it must be divisible by 9.
(b) If a number is divisible by
9, it must be divisible by 3.
(c) A number is divisible by
18, if it is divisible by both 3 and 6.
(d) If a number is divisible
by 9 and 10 both, then it must be divisible by 90.
(e) If two numbers are
co-primes, at least one of them must be prime.
(f) All numbers which are
divisible by 4 must also be divisible by 8.
(g) All numbers which are
divisible by 8 must also be divisible by 4.
(h) If a number exactly
divides two numbers separately, it must exactly divide their sum.
(i) If a number exactly divides
the sum of two numbers, it must exactly divide the two numbers separately.
Solution.
(a) False; Number 21 is divisible by
3 but not by 9.
(b) True; Number 9 = 3 × 3,
which means 3 is a factor of 9.
(c) False; Number 24 is divisible by both 3 and 6 but not by 30.
(d) True; Number 9 × 10 = 90
(e) False; since 18 and 35 are co-primes (they have only 1 as their common multiple) but both of them are composites.
(f) False; Number 20 is divisible by
4 but not by 8.
(g) True; Number 4 is a factor of
8 so all the numbers which are divisible by 8 will also be divisible by 4.
(h) True; Number 3 divides 6
and 9, it also divides 6 + 9 = 15.
(i) False; Since 3 divides 15
but it does not divide 8 and 7.
2.Here are two different
factor trees for 60. Write the missing numbers.
(a)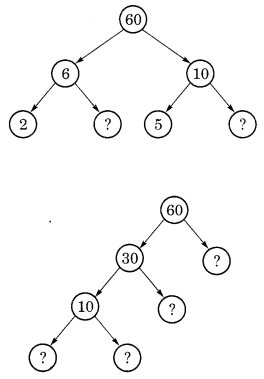
(a) Since 6 = 2 ×3 and 10
= 5 ×2
Missing numbers in the factor
tree of 60 can be filled as follows:
Given that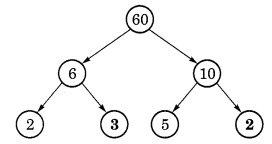
Here, 6 = 2 x missing number
∴ Missing number = 6 2 = 3
Similarly, 10 = 5 x missing number
∴ Missing number = 10 ÷ 5 = 2
Hence, the missing numbers are 3 and 2.
(b) Since 60 = 30 ×2, 30 = 10
×3 and 10 = 5×2
Thus, missing numbers in the factor tree of 60 can be filled as follows:
60 = 30 x m1
⇒ m1 = 60 ÷ 30 = 2
30 = 10 x m2
⇒ m2 = 30 ÷ 10 = 3
10 = m3 x m4
⇒ m3 = 2 or 5 and m4 = 5 or 2
Hence, the missing numbers are 2, 3, 2, 5.
Sum No.3
Which factors are not
included in the prime factorisation of a composite number?
Solution. 1 and the number itself are not included in the prime factorisation of a composite number.
Sum No.4.
Write the greatest 4-digit
number and express it in terms of its prime factors.
Solution.
The greatest 4-digit number =
9999
Its prime factors are
calculated as follows:
The greatest 4-digit number = 9999
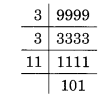
Hence, 9999 can be expressed
in terms of its prime factors as:
9999 = 3 x 3 x 11 x 101.
Sum No 5.
Write the smallest 5-digit
number and express it in the form of its prime factors.
Solution.
The smallest 5-digit number =
10000
Its prime factors are
calculated as follows:
The smallest 5-digit number = 10000
Hence, 10000 can be expressed in terms of its prime factors as:
10000 = 2 x 2 x 2 x 2 x 5 x 5
x 5 x 5.
Sum No.6.
Find all the prime factors
of 1729 and arrange them in ascending order. Now state the relations, if any,
between the two consecutive prime factors.
Solution.
Prime factors of 1729 are
calculated as follows:
Given number = 1729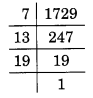
Hence, the prime factors of
1729 = 7 x 13 x 19.
Here, 13 – 7 = 6 and 19 – 13 =
6
We can see that the difference
between two consecutive prime factors is 6.
Sum No 7.
The product of three
consecutive numbers is always divisible by 6. Verify this statement with the
help of some examples.
Solution.
(i) 5, 6, 7
5 × 6 × 7 = 210 which is
divisible by 6.
(ii)
30 x 31 x 32 = 29760 which is divisible by 6.
(iii) 18, 19, 20
18 × 19 × 20 = 6840 which is
divisible by 6.
Sum No 8.
The sum of two consecutive
odd numbers is divisible by 4. Verify this statement with the help of some
examples.
Solution.
(i) 97 + 99 = 196 which is divisible by 4.
(ii) 59 + 61 = 120 which is divisible by 4.
(iii) 105 + 107 = 212 which is divisible by 4.
Sum No 9.
In which of the following expressions, prime factorisation has been done?
(a) 24 = 2 x 3 x 4 (b) 56 = 7 x 2 x 2 x 2
(c) 70 = 2 x 5 x 7 (d) 54 = 2 x 3 x 9.
Solution.
(a) 24 = 2 x 3 x 4
Here, 4 is not a prime number.
Therefore, 24 = 2 x 3 x 4 is
not a prime factorisation.
(b) 56 = 7 x 2 x 2 x 2
Here, all factors are prime
numbers
Therefore, 56 = 7 x 2 x 2 x 2
is a prime factorisation.
(c) 70 = 2 x 5 x 7
Here, all factors are prime
numbers.
Therefore, 70 = 2 x 5 x 7 is a
prime factorisation.
(d) 54 = 2 x 3 x 9
Here, 9 is not a prime number.
Therefore, 54 = 2 x 3 x 9 is
not a prime factorisation.
Sum NO.10.
Determine if 25110 is
divisible by 45.
Solution.
45 = 5 x 9
Now factors of 5 = 1, 5
And factors of 9 = 1, 3, 9
Since, 5 and 9 have only 1 as
common factor so they are co-prime numbers.
Now we will check the
divisibility of 25110 by 5 and 9.
To check divisibility by 5:
As the ones place of the
number 25110 is 0. So, it is divisible by 5.
To check divisibility by 9:
Sum of all the digits of
number 25110 = 2 + 5 + 1 + 1 + 0 = 9 which is divisible by 9.
So, the number 25110 is
divisible by both 5 and 9, so it is also divisible by 45.
Sum No.11.
18 is divisible by both 2
and 3. It is also divisible by 2 x 3 = 6. Similarly, a number is divisible by
both 4 and 6. Can we say that the number must also be divisible by 4 x 6 = 24?
If not, give an example to justify your answer.
Solution.
Here, the given two numbers are not co-prime. So, it is not necessary that a number divisible by both 4 and 6, must also be divisible by their product 4 x 6 = 24.
Example: 36 and 60 are divisible by 4, both 4 and 6 but not by 24.
Sum No 12.
I am the smallest number,
having four different prime factors. Can you find me?
Solution.
We know that the smallest 4 prime numbers are 2, 3, 5 and 7.
Hence, the required number = 2 x 3 x 5 x 7 = 210
Exercise 3.6
Sum No 1.
Find the HCF of the
following numbers:
(a) 18, 48 (b) 30, 42 (c) 18, 60 (d) 27,63 (e) 36,84
(f) 34, 102 (g) 70, 105, 175 (h) 91, 112, 49 (i) 18, 54, 81 (j) 12, 45, 75
Solution.
(a) 18 and 48
18 = 2 x 3 x 3
Hence, the HCF = 2 x 3 = 6.
(b) 30 and 42.
30 = 2 x 3 x 5
42 = 2 x 3 x 7
Here, the common factors are 2 and 3.
Hence, the H.C.F = 2 x 3 = 6.
(c) 18 and 60.
18 = 2
x 3 x 3
60= 2
x 2 x 3 x 5
Here, the common factors are 2 and 3.
Hence, the HCF of 18 and 6 is 2 x 3 = 6.
(d) 27 and 63.
27 = 3 x 3 x 3
63 = 3 x 3 x 7
Here, the common factor is 3 (occurring twice).
Hence, the HCF = 3 x 3 = 9.
(e) 36 and 84.
(f) 34 and 102.
(g) The given numbers are 70, 105 and 175.
(h) 91, 112 and 49.
(i) 18, 54 and 81.
(j) Given numbers are 12, 45 and 75.
(a) numbers? (b) even numbers? (c) odd numbers?
Solution.
(a) Since the common factor of
two consecutive numbers is 1
Hence, the HCF of two
consecutive numbers = 1
(b) Since, the common factors
of two consecutive even numbers are 1 and 2
Hence, the HCF two consecutive
even numbers = 1 x 2 = 2
(c) Since, the common factor
of two consecutive odd numbers is 1
Hence, the HCF of two
consecutive odd numbers = 1
Sum No. 3.
HCF of co-prime numbers 4
and 15 was found as follows by factorisation:
4 = 2 x 2 and 15 = 3 x 15 since there is no common prime factor, so HCF of 4 and 15 is 0. Is the answer correct? If not, what is the correct HCF?
Solution.
No, answer is not correct.
1 is the prime factor of
co-prime numbers.
Hence, the correct HCF of 4
and 15 is 1.
Exercise 3.7
Sum No.1
Renu purchases two bags of
fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight which
can measure the weight of the fertiliser exact number of times.
Solution.
Maximum value of weight = HCF
of 75 and69
Hence, maximum value of weight which can measure the weight of the fertiliser exact number of times = 3 kg.
Sum no 2.
Three boys step off
together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm
respectively. What is the minimum distance each should cover so that all can
cover the distance in complete steps?
Solution.
Minimum distance = LCM of 63,
70, 77
Sum No 3.
The length, breadth and
height of a room are 825 cm, 675 cm and 450 cm respectively. Find the longest
tape which can measure the three dimensions of the room exactly.
Solution.
The longest tape = HCF of 825,
675 and 450
Sum No 4.
Determine the smallest
3-digit number which is exactly divisible by 6, 8 and 12.
Solution.
Smallest number which is
exactly divisible by 6, 8 and 12 = LCM of 6, 8 and 12
But we need to find the smallest three digit number which is divisible by 6, 8 and 12.
Here 24 × 4 = 96 and 24 × 5 =
120
Thus, 120 is the required
smallest three digit number which is exactly divisible by 6, 8 and 12.
Sum No 5.
Determine the greatest
3-digit number exactly divisible by 8, 10 and 12.
Solution.
We first find the LCM of 8, 10
and 12
∴ LCM of 8, 10 and 12 = 2 x 2 x
2 x 3 x 5 = 120
We need to find the greatest
3-digit number exactly divisible by 8, 10 and 12.
Here, 120 x 8 = 960 and 120 x 9 = 1080
Hence, 960 is the required
greatest three digit number.
Sum no 6.
The traffic lights at three
different road crossings change after every 48 seconds, 72 seconds and 108
seconds respectively. If they change simultaneously at 7 a.m., at what time
will they change simultaneously again?
Solution.
Time at which the lights will
change simultaneously = LCM of 48, 72 and 108
Hence, the required time is = 432
seconds = 7 minutes 12 seconds
i.e., the lights will change
simultaneously at 7 minutes 12 seconds past 7 a.m.
Sum No 7.
Three tankers contain 403
litres, 434 litres and 465 litres of diesel respectively. Find the maximum
capacity of a container that can measure the diesel of the three containers
exact number of times.
Solution.
Maximum capacity of the
container = HCF of 403, 434 and 465.
Hence, the maximum capacity of the required container = 31 litres.
Sum No 8.
Find the least number which
when divided by 6, 15 and 18 leave remainder 5 in each case.
Solution.
Least number which is exactly divisible by 6, 15 and
18 = LCM of 6, 15 and 18
So, 90 is the least number exactly divisible by 6, 15 and 18.
To get a remainder 5,
the
least number will be 90 + 5 = 95.
Hence, the required number is
95.
Sum No 9.
Find the smallest 4-digit
number which is divisible by 18, 24 and 32.
Solution.
The smallest number divisible
by 18, 24 and 32 = LCM of 18, 24 and 32
Since, 288 is the smallest number which is exactly divisible by 18, 24 and 32 but it is not a 4-digit number.
or
Now 288 × 3 = 864 and 288 × 4 = 1152
So, the smallest 4-digit number which is divisible by 18, 24 and 32 =1152
Sum no 10.
Find the LCM of the
following numbers:
(a) 9 and 4
(b) 12 and 5
(c) 6 and 5
(d) 15 and 4
Observe a common property in
the obtained LCMs. Is LCM the product of two numbers in each case?
Solution.
(a) 9 and 4
∴ LCM of 9 and 4= 2 x 2 x 3 x 5
= 36
Also 9 x 4 = 36
Thus, LCM of 9 and 4 = Product
of 9 and 4.
(b) 12 and 5
∴ LCM of 12 and 5 = 2 x 2 x 3 x
5 = 60
Also 12 x 5 = 60
Thus, LCM of 12 and 5 =
Product of 12 and 5
(c) 6 and 5
∴ LCM of 6 and 5= 2 x 3 x 5 =
30.
Also 6 x 5 = 30.
Thus, LCM of 6 and 5 = Product
of 6 and 5
(d) 15 and 4
∴ LCM of 15 and 4 = 2 x 2 x 3 x
5 = 60
Also 15 x 4 = 60
Thus, LCM of 15 and 4 =
Product of 15 and 4
Here, in all of the questions
given above the LCM of numbers comes to be equal to their product. Actually,
when two numbers are co-prime their LCM is equal to their product.
Sum no 11.
Find the LCM of the
following numbers in which one number is the factor of the other.
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45
What do you observe in the
results obtained?
Solution.
(a) 5 and 20
∴ LCM of 5 and 20 = 2 x 2 x 5 =
20
Hence, the LCM of 5 and 20 = 20
(b) 6 and 18
∴ LCM of 6 and 18 = 2 x 3 x 3 =
18
Hence, the LCM of 6 and 18 =
18
(c) 12 and 48
LCM of 12 and 48 = 2 x 2 x 2 x
2 x 3 = 48
Hence, the LCM of 12 and 48 =
48
(d) 9 and 45
∴ LCM of 9 and 45= 3 x 3 x 5 =
45
Hence, the LCM of 9 and 45 =
45
Here is all the questions
given above, we observe that the LCM of the two numbers, with one number being
a factor of the other, is the greater number.
































No comments:
Post a Comment